Dinâmica Newtoniana

Posted Sep 18, 2024 Updated Oct 1, 2024

By Leandro Gonzaga Peres

views 17 min read

Neste segundo post, da série sobre física deste humilde blog, vamos entender como objetos se movem usando vetores, de forma simples e interativa. A ideia aqui agora é abordar conceitos básicos da mecânica newtoniana e mostrar como podemos aplicar esses princípios para descrever o movimento a fim de criar nossa primeira simulação de partículas.

Em resumo: vamos usar a mecânica newtoniana básica e vetores para mover as coisas!

Introdução à Mecânica Clássica

A mecânica clássica é uma área da física que estuda o movimento dos corpos e as forças que agem sobre eles. Tendo como destaque o Isaac Newton no século XVII, ela fornece um “framework” teórico para descrever e prever o comportamento de objetos físicos em escalas observáveis. Baseando-se em conceitos como posição, velocidade, aceleração, massa e força, a mecânica newtoniana utiliza ferramentas matemáticas, incluindo cálculo diferencial e integral, para analisar sistemas físicos.

Mas não se preocupe com essas últimas palavras ~chiques~. Vamos por partes.

Dinâmica Newtoniana

Sendo direta e muito eficiente para descrever fenômenos cotidianos, ela se baseia em três leis fundamentais:

Inércia: Um objeto permanece em repouso ou em movimento retilíneo uniforme, a menos que uma força externa atue sobre ele. Isso explica a tendência natural de objetos manterem seu estado de movimento, como o seu repouso.
Força e Aceleração: A força aplicada sobre um objeto é proporcional à sua massa e à aceleração resultante. Essa relação, expressa pela fórmula \(F = m \cdot a\), permite calcular o efeito das forças nos corpos.
Ação e Reação: Para cada ação, há uma reação de mesma intensidade e em direção oposta. Isso explica, por exemplo, por que, ao empurrar o chão, o chão exerce uma força igual e contrária sobre você, permitindo que você ande.

Além de Newton: Lagrange e Hamilton

Embora poderosa e bastante útil para nossos estudos, a mecânica newtoniana não consegue solucionar todos os cenários. Em sistemas mais complexos, especialmente aqueles com múltiplos graus de liberdade, a mecânica lagrangiana se destaca como uma alternativa eficiente. Baseada no conceito de energia e no princípio da menor ação, essa abordagem simplifica o estudo de sistemas onde o cálculo direto das forças é desafiador — e quando não é, não é mesmo? —, proporcionando, assim, uma nova perspectiva na compreensão da dinâmica.

A mecânica hamiltoniana, por outro lado, oferece uma visão mais profunda dos sistemas dinâmicos, focando na energia total do sistema. Essa abordagem é especialmente útil para entender fenômenos de conservação de energia e prever o comportamento de sistemas ao longo do tempo.

Ao mergulhar nas diferentes formulações da mecânica clássica, você não apenas compreende melhor o movimento dos corpos no mundo real, mas também expande suas possibilidades criativas para desenvolver simulações, jogos e soluções que desafiam os limites da física cotidiana.

Bom… sei que é muita informação para absorver de uma só vez, especialmente com as diferentes abordagens da mecânica clássica — e acredite, como entusiasta, já tive minha cabeça explodida algumas vezes ao estudar um pouco da Lagrangiana. Mas, vamos nos ater ao básico: a mecânica newtoniana. Ela é simples e eficiente para simular movimentos e colisões em jogos. Com suas três leis, você já pode começar a entender e implementar as bases de um motor de física. Não se preocupe em dominar tudo de uma vez; começamos com Newton e vamos avançando aos poucos.

Posição

Na vida mundana, todos nós temos uma noção do conceito de posição. Quando você diz a um amigo onde está sentado em uma sala de aula ou descreve a localização de um objeto em sua casa, você está, de fato, falando sobre posição e fornecendo coordenadas.

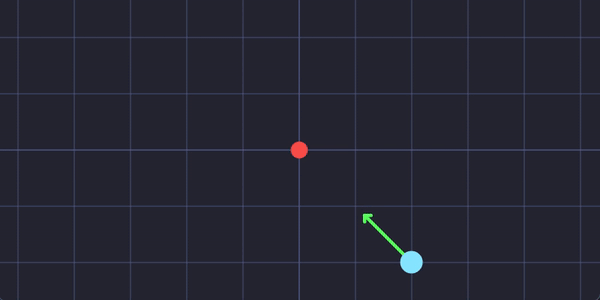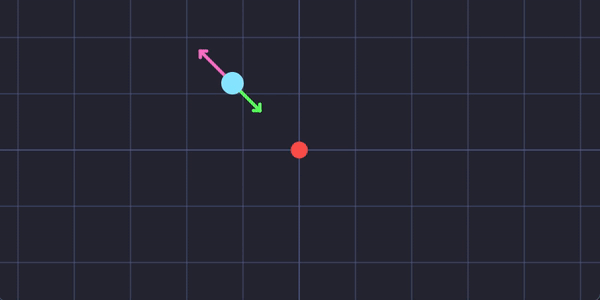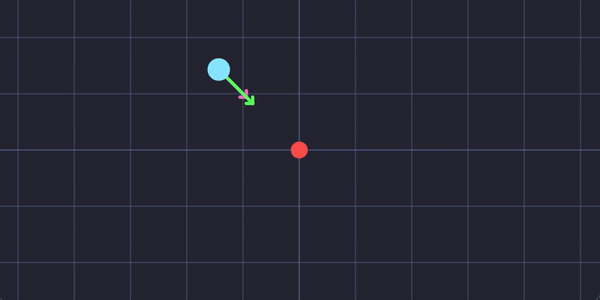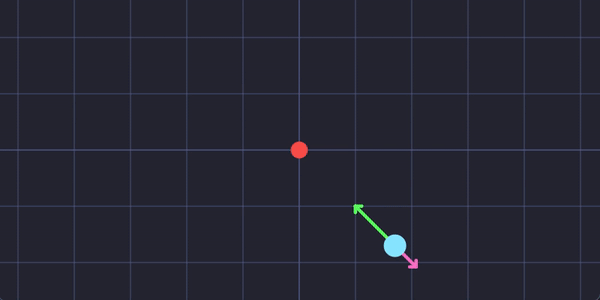
Na física, usamos vetores para descrever a posição de forma mais precisa. Um vetor de posição é simplesmente uma seta que vai de um ponto de referência (que chamamos de origem) até o objeto em questão.

Na demonstração acima, a origem é colocada no centro, o eixo x vai da esquerda para a direita e o eixo y vai de baixo para cima. Você pode mover a posição clicando na tela.

É importante entender que a posição é sempre relativa a um ponto de referência. Por exemplo, o sistema de referência muda a percepção de movimento para quem está dentro de um ônibus em movimento e para quem está parado na rua observando tal ônibus.

Começamos a construir nossa engine de física com partículas 2D. O primeiro passo em C++ é declarar a classe dos Vetores:

  
struct Vector2D
{
  float x, y;

  Vector2D
  operator+ ( const Vector2D & v ) const
  {
    return { x + v.x, y + v.y };
  }

  Vector2D
  operator- ( const Vector2D & v ) const
  {
    return { x - v.x, y - v.y };
  }

  Vector2D
  operator* ( const float & n ) const
  {
    return { x * n, y * n };
  }

  /** ... */
};

struct Particle
{
  Vetor2D pos = { 0, 0 }; // Posição da partícula
};

Velocidade

A velocidade é a taxa de mudança da posição em relação ao tempo. Em outras palavras, é quão rápido e em que direção um objeto está se movendo. Matematicamente, podemos expressar isso como:

\[\vec{V} = \frac{\vec{\Delta p}}{\Delta t}\]

Onde:

\(\vec{V}\) é a velocidade (um vetor)
\(\vec{\Delta p}\) é a mudança na posição (também um vetor)
\(\Delta t\) é o intervalo de tempo

Agora, a posição se move com base na velocidade. Clique para mudar a direção.

Você entende que a velocidade é um vetor, o que significa que ela tem tanto magnitude (“rapidez”) quanto direção. Por exemplo, um carro viajando a 60 km/h para o norte tem uma velocidade diferente de um carro viajando a 60 km/h para o sul, mesmo que ambos estejam se movendo com a mesma magnitude.

Em nossao sistema de parículas, basta adicionar à posição a velocidade multiplicada pelo delta time – ou o tempo de processamento do quadro. Isto é de grande importância para manter a continuidade no movimento, garantindo que as partículas se movam de maneira consistente e proporcional ao tempo, independentemente da taxa de quadros por segundo (FPS). Assim, o movimento das partículas não parecerá mais rápido ou mais lento caso haja varância na taxa de quadros, favorecendo uma simulação mais realista e fluida.

  
struct Particle
{
  Vetor2D pos;      // Posição do corpo
  Vetor2D vel;      // Velocidade do corpo

  void
  Integrate( float dt )
  {
    pos = pos + ( vel * dt ); // Atualiza a posição com base na velocidade
  }
};

Aceleração

Continuando nossa jornada, chegamos ao conceito de aceleração. Experimentamos aceleração quando um carro arranca no semáforo ou quando um elevador começa a subir. Aceleração é a taxa de mudança da velocidade em relação ao tempo.

Matematicamente, podemos expressar a aceleração assim:

\[\vec{a} = \frac{\vec{\Delta v}}{\Delta t}\]

Onde:

\(\vec{a}\) é a aceleração (um vetor)
\(\vec{\Delta v}\) é a mudança na velocidade (também um vetor)
\(\Delta t\) é o intervalo de tempo

Simulação de forças aplicadas a um objeto, com visualização de velocidade, aceleração e dados gráficos. Clique ou arraste para definir um novo alvo.

  
struct Body
{
  Vetor2D pos;      // Posição do corpo
  Vetor2D vel;      // Velocidade do corpo
  Vetor2D acel;     // Aceleração do corpo

  void
  IntegrateVelocities( float dt )
  {
    vel = vel + (acel * dt); // Atualiza a velocidade com base na aceleração
    pos = pos + (vel * dt);  // Atualiza a posição com base na nova velocidade
  }
};

Integração

Como leitor atento, você certamente visualizou as relações fundamentais: a taxa de variação da posição corresponde à velocidade, enquanto a taxa de variação da velocidade define a aceleração. Podemos, no entanto, analisar esses conceitos sob uma outra perspectiva: a posição de um objeto em determinado instante resulta do acúmulo dos efeitos da velocidade ao longo do tempo, ao passo que sua velocidade nesse mesmo momento é consequência do acúmulo dos efeitos da aceleração durante o período considerado.

Como exemplo, visualize um carro que está se movendo a 100 km/h na direção ao norte \(\uparrow\) por 2 horas. Logo, ele deve estar a 200 km a norte de seu ponto de partida. Esta é a ideia mais básica da integração. Uma integral representa o acúmulo da taxa de mudança ao longo de uma janela de tempo, no nosso caso.

A diferenciação está associada à noção de diferença, capturando a taxa instantânea de variação, enquanto a integração se relaciona com o conceito de soma, acumulando essas variações ao longo do tempo. Em verdade, a origem do símbolo da integral \(\int\) remonta a um “S” estilizado, derivado do termo latino “summa”, que significa “soma” ou “total”.

Área e Integração

A integração pode ser visualizada geometricamente como a área sob uma curva em um gráfico. Para ilustrar, examinemos a relação entre velocidade e posição. Quando a velocidade é constante, a variação na posição é calculada pelo produto da velocidade pelo tempo decorrido. Esta relação é representada graficamente pela área da região sombreada no gráfico abaixo.

Velocidade constante (linha azul) e variação na posição (área sombreada).

Se traçarmos o gráfico da área, ele ficará assim. Este é o gráfico da integral da velocidade, que representa a mudança na posição ao longo do tempo. Quando a velocidade é constante, o gráfico da posição se torna uma linha reta.

Posição ao longo do tempo com velocidade constante (linha vermelha).

Pode não ser tão óbvio quando o gráfico não é reto. Mas se você imaginar que a forma consiste em muitas faixas retangulares estreitas, você pode aproximar sua área. Integração é o acúmulo de mudança ao longo do tempo. Você pode pensar em cada faixa como uma aproximação do efeito da velocidade em um curto período de tempo. Ao somar as áreas de todas as faixas, você pode encontrar a quantidade total de mudança.

Os métodos de soma de Riemann nos ajudam a estimar áreas sob curvas, demonstrando como diferentes abordagens podem influenciar a precisão das aproximações.

Integração Numérica

O próximo passo, de acordo com livros de matemática comuns, seria tornar essas faixas infinitamente estreitas, De tal modo que as tornem cada vez mais próximas do formato original do gráfico. Entretanto, ao calcular integração em um computador e em aplicação que requerem performance em tempo real, é muito custoso, tomando tempo de execução valiosos. Então, geralmente é mais prático aproximá-la escolhendo uma largura pequena o suficiente para janela da análise.

Por enquanto, na data em que escrevo este post, não entrarei em maiores detalhes. Talvez eu aborde isso em uma atualização futura.

Método de Euler

Em jogos de computador ou animações, frequentemente usamos o Método de Euler para atualizar a posição de um objeto quadro a quadro. Isso envolve adicionar a velocidade (ou velocidade multiplicada pelo tempo) à posição atual a cada quadro. Esse método, com o qual você já deve estar familiarizado, também pode ser visto como uma aproximação numérica de uma integral.

Para visualizar o método de Euler em ação, verifique a interação na seção Velocidade demonstrada anteriormente.

Existem versões aprimoradas do método de Euler, como o Método de Runge-Kutta, que são reconhecidas como técnicas bem mais avançadas de integração numérica. No entanto, como não abordaremos esse tópico em detalhe aqui, recomendo consultar outras fontes para um entendimento mais profundo.

Força e Massa

Agora que compreendemos a posição, a velocidade e a aceleração, bem como a integração desses conceitos, podemos avançar para o cerne da dinâmica newtoniana: a relação entre força, massa e aceleração.

Como mencionado mais cedo, Isaac Newton sintetizou essa relação em sua Segunda Lei do Movimento, que pode ser expressa matematicamente como:

\[\vec{F} = m \cdot \vec{a}\]

Onde:

\(\vec{F}\) é a força resultante (um vetor)
\(m\) é a massa do objeto (um escalar)
\(\vec{a}\) é a aceleração (um vetor)

Esta equação nos diz que a força resultante aplicada a um objeto é igual ao produto de sua massa pela aceleração que ela produz.

A aceleração dos objetos é inversamente proporcional à massa, conforme a relação a = F/m, direcionando-os ao cursor.

Note que quanto maior a massa de um objeto, maior será a força necessária para mudar seu estado de movimento.

Inverso da Massa

Ao rearranjar a equação de Newton, podemos expressar a aceleração em termos da força e da massa do objeto. Isso é essencial para as simulações em engines de física, pois nos permite calcular como um objeto deve acelerar quando submetido a uma força resultante.

\[\vec{a} = \vec{F} \cdot \frac{1}{m}\]

Em engines de física, é comum armazenar a inversa da massa para auxiliar nos cálculos, especialmente quando há múltiplos objetos interagindo. Utilizar a inversa da massa (ou seja, \(\frac{1}{m}\)) evita operações de divisão repetitivas e facilita a manipulação de corpos com massa infinita, como objetos imóveis, para os quais a inversa da massa é simplesmente zero.

  
struct Body
{
  Vetor2D pos;        // Posição do corpo
  Vetor2D vel;        // Velocidade do corpo
  Vetor2D acel;       // Aceleração do corpo
  float   invMass;    // Inverso da massa do corpo. 0, caso infinito (static/kinematic)
  Vetor2D netForces;  // Força resultante aplicada no corpo

  void
  AddForce( const Vetor2D & f )
  {
    netForces += f;              // Adiciona a força à força resultante
  }

  void
  IntegrateForces( float dt )
  {
    acel = netForces * invMass;  // Calcula a aceleração com base na força resultante e no inverso da massa
    netForces = { 0.0F, 0.0F };  // Reseta a força resultante após a integração
  }

  void
  IntegrateVelocities( float dt )
  {
    vel = vel + (acel * dt);     // Atualiza a velocidade com base na aceleração
    pos = pos + (vel * dt);      // Atualiza a posição com base na nova velocidade
  }

  /** ... */
};

Múltiplas forças

Quando diversas forças atuam sobre um objeto, a força resultante é a soma vetorial de todas as forças individuais. Isso pode ser expresso da seguinte forma:

\[F_{\text{total}} = \sum F_i\]

Onde \(F_{\text{total}}\) é a força resultante e \(F_i\) representa cada força aplicada. Compreender essa relação é crucial para analisar sistemas mais complexos e prever o movimento resultante.

A letra do alfabeto grego Sigma, ∑, ou mesmo o Π, parecem-lhe uns símbolos estranhos e amedrontadores? Veja só a imagem abaixo e você, programadore, nunca mais se assustará: Por @FreyaHolmer

Gravidade

Um dos exemplos mais comuns de força na natureza é a gravidade. Todos os objetos com massa exercem uma atração gravitacional uns sobre os outros. Na superfície da Terra, a gravidade é uma força constante que atrai os objetos em direção ao centro do planeta.

Simulação de queda livre de um corpo com gráficos que mostram a posição, velocidade e aceleração ao longo do tempo.

Você sabia que objetos de diferentes massas caem na mesma velocidade no vácuo? Esse fenômeno, inicialmente teorizado por Galileu Galilei no século XVII, ocorre porque a aceleração gravitacional é a mesma para todos os objetos, independentemente de sua massa. Galilei desafiou a crença aristotélica, que predominou por mais de dois milênios e afirmava que objetos mais pesados cairiam mais rápido. Embora a força gravitacional seja proporcional à massa de cada objeto, a inércia (resistência à aceleração) também aumenta proporcionalmente, resultando na mesma aceleração para todos os corpos em queda livre no vácuo.

Se combinarmos tudo que vimos até aqui, e ajustarmos para imprimir o instante da posição, temos:

Gravitação universal

A gravidade da Terra é apenas uma manifestação da força gravitacional universal que age entre todos os objetos. Todos os objetos são atraídos uns pelos outros, e a magnitude dessa atração é expressa pela seguinte equação:

\[{\displaystyle F=G{\frac {m_{1}m_{2}}{r^{2}}}\ }\]

Onde:

\(m_1\) e \(m_2\) são as massas dos respectivos objetos
\(G\) é a constante gravitacional, que vale aproximadamente \(6{,}6743 \times 10^{-11} \, \text{m}^3 \, \text{kg}^{-1} \, \text{s}^{-2}\)
\(r\) é a distância entre os centros dos objetos.

Em um corpo celeste como a Terra, apenas a força de queda em direção ao seu centro é percebida como gravidade, já que esse corpo é geralmente muito mais pesado do que tudo ao redor. Note que o termo “gravidade” pode se referir tanto a essa força descendente específica quanto à força universal entre todos os objetos, dependendo do contexto.

A demonstração abaixo é uma simulação simples da força gravitacional universal atuando entre objetos com massas diferentes. Porém, como não somos astrônomos buscando uma simulação 1:1, uma simulação exata da realidade, podemos alterar ao nosso bel prazer, como adicionar repulsão.

Simulação de corpos gravitacionais com controle de massa, quantidade e alternância entre atração e repulsão.

Para ajustar nossa engine de partículas, calculamos a força resultante entre os corpos e aplicamos em ambos:

  
#include <iostream>
#include <cmath>  /** sqrt */

#include "particle.h"

constexpr double G = 6.67430e-11;   // Constante gravitacional
constexpr double dt = 1.0 / 60.0;   // Passo de tempo para simulação

Vector2D
CalculateGravitationalForce( const Particle & p1, const Particle & p2 )
{
  Vector2D direction = p1.pos - p2.pos;
  double distance = direction.Magnitude();
  if (distance > 1.0)  // Evitar divisão por zero
  {
    double forceMagnitude = G / (p1.invMass * p2.invMass) / (distance * distance);
    return direction.Normalize() * forceMagnitude;
  }
  return { 0.0, 0.0 };
}

void
SimulateOrbit( Particle & planet, Particle & satellite, int steps )
{
  for (int i = 0; i < steps; ++i)
  {
    Vector2D force = CalculateGravitationalForce( planet, satellite );
    
    satellite.AddForce( force );
    planet.AddForce( force * -1.0 );

    satellite.Update( dt );
    planet.Update( dt );

    if (i % 60 == 0)
    {
      printf("t: %.2f - Posição do Satélite (X, Y): %.6f, %.6f\n", i * dt, satellite.pos.x, satellite.pos.y);
    }
  }
}

int main()
{
  Particle planet { 0 };
  planet.pos       = { 0.0, 0.0 }; // No centro
  planet.vel       = { 0.0, 0.0 }; // Sem velocidade inicial
  planet.acel      = { 0.0, 0.0 }; // Sem aceleração inicial
  planet.invMass   = 1.0F / 5e10;  // Massa grande
  planet.netForces = { 0.0, 0.0 }; // Sem forças iniciais

  // Partícula 2: Satélite (massa menor)
  Particle satellite { 0 };
  satellite.pos       = { 100.0, 0.0 };  // Iniciando a certa distância do planeta
  satellite.vel       = { 0.0, 100.0 };  // Velocidade inicial para órbita
  satellite.acel      = { 0.0, 0.0 };    // Sem aceleração inicial
  satellite.invMass   = 1.0F / 100.0F;   // Massa menor
  satellite.netForces = { 0.0, 0.0 };    // Sem forças iniciais

  // Simulação por 10 segundos
  SimulateOrbit( planet, satellite, 60 * 10 );

  return 0;
}

Pela Terceira Lei de Newton, toda força gera uma reação de igual intensidade, mas no sentido oposto. Isso significa que, ao aplicarmos uma força positiva em um corpo, devemos aplicar uma força negativa de mesma magnitude no outro corpo envolvido na dinâmica, garantindo, assim, o equilíbrio entre as forças.

Physics, Portuguese

Physics Game Development

This post is licensed under CC BY 4.0 by the author.

Introdução à Mecânica Clássica

Dinâmica Newtoniana

Além de Newton: Lagrange e Hamilton

Posição

Velocidade

Aceleração

Integração

Área e Integração

Integração Numérica

Método de Euler

Força e Massa

Inverso da Massa

Múltiplas forças

Gravidade

Gravitação universal

Trending Tags